Columnar Transposition Cipher

Introduction 

The columnar transposition cipher is a fairly simple, easy to implement cipher. It is a transposition cipher that follows a simple rule for mixing up the characters in the plaintext to form the ciphertext.

Although weak on its own, it can be combined with other ciphers, such as a substitution cipher, the combination of which can be more difficult to break than either cipher on it's own. The ADFGVX cipheruses a columnar transposition to greatly improve its security.



Example 

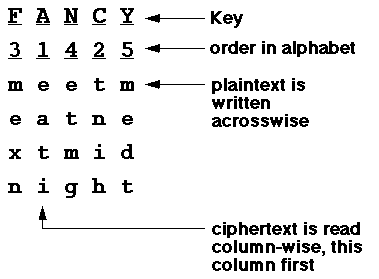
The key for the columnar transposition cipher is a keyword e.g. GERMAN. The row length that is used is the same as the length of the keyword. To encrypt a piece of text, e.g.
defend the east wall of the castle

we write it out in a special way in a number of rows (the keyword here is GERMAN):
G E R M A N
d e f e n d
t h e e a s
t w a l l o
f t h e c a
s t l e x x

In the above example, the plaintext has been padded so that it neatly fits in a rectangle. This is known as a regular columnar transposition. An irregular columnar transposition leaves these characters blank, though this makes decryption slightly more difficult. The columns are now reordered such that the letters in the key word are ordered alphabetically.
A E G M N R
n e d e d f
a h t e s e
l w t l o a
c t f e a h
x t s e x l

The ciphertext is read off along the columns:
nalcxehwttdttfseeleedsoaxfeahl

Plain Text:-attack at dawn


keyword = zebra              pad character = x

Chiphertext:-caxttxtanadxakw





Code:-

#python3 code for Columnar Cipher TransFormation made by Quid Zohar Morbiwala

key=input ('Enter a key ') 
userval=input ('Enter a value ')
col=len(key)
if((len(userval)%col)!=0):userval+="x"*(len(userval)%col)
userval=userval.replace(' ', '')#remove white spaces from key 
o=[]
for i in key:
 o.append(i)  #generating list for keys
h=[]
for i in range(col):
 h.append(userval[i:len(userval):col])#generating list for plaintext column wise 
dic=dict(zip(o,h))    #adding both lists
so=sorted(dic.keys())    #sorting alphabateically keys of cipher
print(''.join(dic[i]for i in so))#join func for displaaying in string format

Output:-

Enter a key GERMAN

Enter a value defend the east wall of the castle

nalcxehwttxdttfsxeeleedsoaxfeahl